Demystifying LLMs With Some Simple Python
TL;DR: Large Language Models (LLMs) like
Gemini or ChatGPT seem to “understand” our questions and “reason” out their
answers. In reality, they don’t have any inherent
understanding. They predict the next word by leveraging complex statistical
associations learned from vast amounts of text.
In this post, we’ll build a toy model that mimics some of these statistical approaches – without any machine learning – just counting letter and word frequencies. We’ll see how even these simple methods can generate text that looks somewhat plausible. Our goal is to highlight that behind the slick, human-like output lies a system that’s fundamentally based on statistical pattern prediction, not genuine reasoning.
Introduction
Modern LLMs are marvels of contemporary artificial intelligence, trained on trillions of words to produce eerily human-like text. But what does “understanding” mean here? At their core, these models:
- Look at the text input (prompt).
- Use learned statistical patterns to predict what’s the most likely next word (or token).
- Continue doing so repeatedly to form what appears to be a coherent response.
They do not have a mind’s eye picturing the scenario, nor a grounded understanding of what they’re talking about. Even when they solve complex tasks, what they’re really doing is pattern-matching based on pre-ingested data.
To illustrate this, let’s start from scratch and build a simple statistical generator. We’ll use a fairly small (by LM standards) set of text as our “training data” and generate text using progressively more complex patterns - from single-letter probabilities to word-level predictions.
1: Data Preparation and Loading
First, we need a source text. Maybe download some Wikipedia articles or delve into the Project Gutenberg archive and store locally as sample.txt - here’s my one cleaned up to remove the boilerplate text at the start and end of each file:
08:18:47
User@AN20 ~/Demystifying LLMs 127 0 😊 $ wc
-w in/*
64229 in/Bridgman - The logic of modern physics.txt
79751 in/Engels - Anti-Duehring.txt
121981 in/Hegel - Philosophy of Mind.txt
86847 in/Kafka - The Trial.txt
113967 in/Nietzsche - Thus Spake Zarathustra.txt
41172 in/Russell - The Practice and Theory of Bolshevism.txt
566328 in/Tolstoy - War and Peace.txt
1074275 total
08:18:50
User@AN20 ~/Demystifying LLMs 130 0 😊 $ > sample.txt &&
for file in in/*.txt; do sed -n '/\\*\\*\\* START OF
THE PROJECT GUTENBERG EBOOK/,/\\*\\*\\* END OF THE
PROJECT GUTENBERG EBOOK/{//!p}' "$file" >> sample.txt; done
08:18:53
User@AN20 ~/Demystifying LLMs 133 0 😊 $ wc
-w sample.txt
1052840 sample.txt
(I wanted about a million words so combined several
classics).
Point the code below to where you have your sample.txt. Make sure your chosen sample text is plain text without any markup.
with open('sample.txt', 'r', encoding='utf-8') as f:
text = f.read().lower()
# Basic cleaning: only keep letters and spaces
text = re.sub(r'[^a-z\s]', '', text)
text = re.sub(r'\s+', ' ', text).strip()
2: Simple Letter Frequency
Let’s start at the simplest possible level. We’ll count how often each letter appears and then generate text by sampling letters according to their overall frequency. This will produce complete gibberish - just a jumble of letters. But it illustrates a key point: if we randomly choose letters based on how common they are, we’ll reproduce the “statistical fingerprint” of the language at a letter level, but no meaningful words.
letters = [ch for ch in text if ch.isalpha()]
letter_counts = Counter(letters)
total_letters = sum(letter_counts.values())
def sample_letter():
r = random.randint(1, total_letters)
cumulative = 0
for l, c in letter_counts.items():
cumulative += c
if cumulative >= r:
return l
print("Random
letters (simple frequency):")
print(''.join(sample_letter() for _ in range(50)))
print()
Here’s what we get:
Random letters (simple frequency):
hronemnlsargnsrhdeihzeoeselagneshahemilnarcnteveiu
3: Predicting the Next Letter
Next, we introduce a small bit of structure; given a letter, we’ll guess what the next letter is likely to be. To do this, we’ll build a Markov chain, of sorts, counting how often each letter follows another letter. This will start to produce letter combinations that are more common in English - like “th” or “an” - and reduce nonsense like “zxq”.
# Build letter -> next-letter counts
letter_follow_counts = defaultdict(Counter)
for i in range(len(letters)-1):
current_letter = letters[i]
next_letter = letters[i+1]
letter_follow_counts[current_letter][next_letter] += 1
def sample_next_letter(prev_letter):
if prev_letter not in letter_follow_counts or len(letter_follow_counts[prev_letter]) == 0:
# fallback
return random.choice(list(letter_counts.keys()))
cdict = letter_follow_counts[prev_letter]
total = sum(cdict.values())
r = random.randint(1, total)
cumulative = 0
for l, cnt in cdict.items():
cumulative += cnt
if cumulative >= r:
return l
current = random.choice(letters)
generated_letters = [current]
for _ in range(50):
current = sample_next_letter(current)
generated_letters.append(current)
print("Letter-based
Markov chain text:")
print(''.join(generated_letters))
print()
You might start seeing more plausible letter pairings like the, ent, ion. Still, we’re likely to get nonsense, but at least it “feels” more language-like at the letter level:
Letter-based Markov chain text:
allethithindeertwhoutitheyberesforsineointogewisofa
4: Building Up to Words
Letters alone are too low-level. What if we move to words? Let’s split our text into words and count their frequencies. We’ll do something similar: start by just sampling words at random based on frequency. This will produce a list of common words (like “the”, “and”, “of”, “to”) but in a random order - no cohesion at all.
words = text.split()
word_counts = Counter(words)
total_words = sum(word_counts.values())
def sample_word():
r = random.randint(1, total_words)
cumulative = 0
for w, c in word_counts.items():
cumulative += c
if cumulative >= r:
return w
print("Random
words (simple frequency):")
print(' '.join(sample_word() for _ in range(sentence_length)))
print()
This will be repetitive and likely full of common English filler words, depending on the input source text of course, but no grammatical sense:
Random words (simple frequency):
there the evening surprise that as one i here polish with you the out days thousand who then the book
5: Word-Level Markov Chains
Let’s now build a Markov model at the word level. We’ll count which words tend to follow other words. This will start to produce text that, while still nonsensical, may form short recognizable phrases. For example, it might consistently place “of” after “part”.
word_follow_counts = defaultdict(Counter)
for i in range(len(words)-1):
current_word = words[i]
next_word = words[i+1]
word_follow_counts[current_word][next_word] += 1
def sample_next_word(prev_word):
if prev_word not in word_follow_counts or len(word_follow_counts[prev_word]) == 0:
return random.choice(list(word_counts.keys()))
cdict = word_follow_counts[prev_word]
total = sum(cdict.values())
r = random.randint(1, total)
cumulative = 0
for w, cnt in cdict.items():
cumulative += cnt
if cumulative >= r:
return w
current = random.choice(words)
generated_sentence = [current]
for _ in range(sentence_length - 1):
current = sample_next_word(current)
generated_sentence.append(current)
print("Word-based
Markov chain sentence:")
print(' '.join(generated_sentence))
print()
We might start to get longer, more coherent phrases:
Word-based Markov chain sentence:
thy poisons political and involuntarily came every man was right to find a populace type they want to know they said
6: Extending the Context
To improve coherence further, we could look at n-grams: pairs or triplets of previous words instead of just one. For example, if we consider two words as context, we might get more stable phrases. Increasing the “order” of the Markov chain will produce more locally coherent text, but still no real meaning.
trigram_counts = defaultdict(Counter)
for i in range(len(words)-2):
pair = (words[i], words[i+1])
next_word = words[i+2]
trigram_counts[pair][next_word] += 1
def sample_trigram_word(prev_two_words):
if prev_two_words not in trigram_counts or len(trigram_counts[prev_two_words]) == 0:
return random.choice(list(word_counts.keys()))
cdict = trigram_counts[prev_two_words]
total = sum(cdict.values())
r = random.randint(1, total)
cumulative = 0
for w, cnt in cdict.items():
cumulative += cnt
if cumulative >= r:
return w
start_index = random.randint(0, len(words)-3)
current_pair = (words[start_index], words[start_index+1])
generated_trigram_sentence = list(current_pair)
for _ in range(sentence_length - 2):
next_w = sample_trigram_word(current_pair)
generated_trigram_sentence.append(next_w)
current_pair = (current_pair[1], next_w)
print("Trigram-based
sentence:")
print(' '.join(generated_trigram_sentence))
This should produce more structured phrases, maybe something that almost looks like part of a legible sentence, but still often nonsensical or stuck in loops:
08:31:36
User@AN20 ~/Demystifying LLMs 896 0 😊 $ time python gentext.py 30
Random letters (simple frequency):
halgstwtsrmtlsaeitsyeeaenaeshahfnrgeriudrarpoiktit
Letter-based Markov chain text:
ypffrmpadolkndswhereerevllebeanlagosumattoursustind
Random words (simple frequency):
it then the eagerly in leaving in why will
he on the those oftener at back that now else
does flattered would
power at the hill smoking virtues been the
Word-based Markov chain sentence:
and see the waist a game to reply we shall help you laugh
at all too many years then dispersed to him of selfish isolation as possible he
checked whether
Trigram-based sentence:
maid of honor he asked pointing
upwards with his involuntary grin caused by englands
intrigues to thank the old communal lands of the people it was becoming more
and more
real 0m7.241s
user 0m0.000s
sys 0m0.000s
This isn’t too dissimilar to your mobile phone’s autocomplete if you keep selecting the first suggested word.

Key Takeaway
All these steps rely purely on counts of what follows what. There’s no “understanding” or “reasoning” going on. Our toy model is extremely simplistic compared to a modern LLM, which uses:
- Massive training data: Trillions of words instead of a few paragraphs.
- Complex tokenization: Instead of just letters or words, sub-word tokens and embeddings are used.
- Neural networks: Transformers are essentially sophisticated pattern-recognition statistical models. They use “attention” to focus on certain parts of the text more than others, enabling them to capture context and produce more coherent predictions.
- Fine-tuning and RLHF (Reinforcement Learning from Human Feedback): Aligning model output with human preferences. With a lot of work having been done by low paid workers in the Global South.
Yet, the fundamental principle is the same: these models find statistical patterns and use them to predict the next token. The illusion of reasoning emerges from the complexity and scale of these statistical patterns. When you have enough data and a sufficiently powerful model, you get text that’s not just plausible at a local level (like bigrams or trigrams) but globally coherent and contextually appropriate. But remember: no matter how real it feels, there’s no entity “thinking” behind the text. There’s just a probability machine, trained at a massive scale.
LLM’s can use language form extremely well but not language meaning (Bender & Koller, 2020) - the following diagrams illustrate this point:
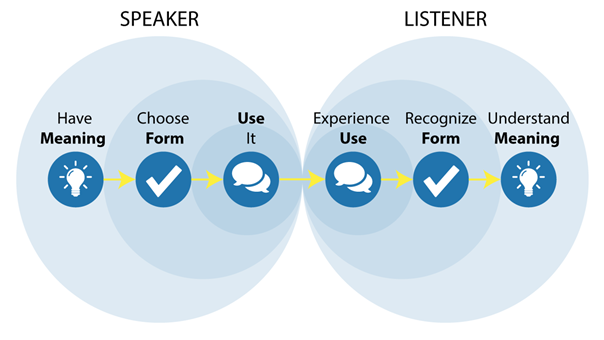
(image courtesy of Real Grammar, 2021)
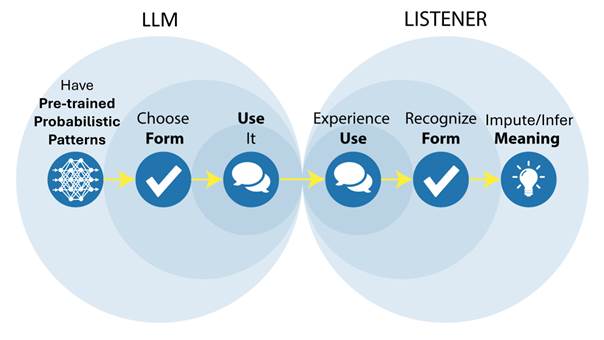
Conclusion
We started with a toy model that generates text from pure frequency counts at the letter level and progressed to a simple Markov chain at the word (and n-gram) level. Even with these simple approaches, we can generate superficially “language-like” text. The gap between our toy and a modern LLM is huge, but the core principle is similar.
LLMs are useful tools – they can assist in coding, writing, and more. But it’s important to remember what they are: stochastic parrots, not thinking agents with beliefs, or understanding. The “intelligence” we perceive is an emergent property of patterns and scale.
In short: LLMs cannot reason in the human sense - they just generate text that is statistically likely. Our simple code demo demystifies them by showing how far you can get just by counting occurrences and probabilities. The difference between our naive system and a commercial LLM is not a change in fundamental principle, but in complexity, scale, and optimization.
References
The term "stochastic
parrot" was introduced in the excellent 2021 paper "On the
Dangers of Stochastic Parrots: Can Language Models Be Too Big?" by
Emily M. Bender, Timnit Gebru, Angelina McMillan-Major, and Margaret Mitchell.
This seminal work critiques large language models (LLMs), highlighting concerns
about their scalability, environmental impact, and inherent biases. ACM Digital
Library
The main
author had previously co-authored another influential paper, “Climbing
towards NLU: On Meaning, Form, and Understanding in the Age of Data" (Emily
M. Bender, Alexander Koller, ACL 2020). The authors distinguish between form
(surface patterns in text) and meaning (the underlying concepts and
relationships). They argue that current language models (from BERT to GPT3) learn form-based correlations and do not achieve what we would call
true “understanding” or reasoning – only pattern recognition that gives an
illusion of comprehension. ACL Anthology
"Large
Language Models Are Not Strong Abstract Reasoners" (Gendron et al, 2023) evaluates LLMs
on abstract reasoning tasks, revealing that despite their proficiency in
various NLP tasks, LLMs exhibit very limited performance in abstract reasoning.
ARXIV
The article "Stochastic
Parrots: How NLP Research Has Gotten Too Big" (Esther Sánchez García
and Michael Gasser, 2021) discusses the implications of large-scale natural
language processing research, emphasizing the potential risks and ethical
considerations associated with developing and deploying extensive language
models. Science for the
People Magazine
For a
comprehensive analysis of LLMs, Felix Morger's 2024 thesis, "In the
Minds of Stochastic Parrots: Benchmarking, Evaluating and Interpreting Large
Language Models", delves into the evaluation and interpretation of
these models, providing insights into their capabilities and limitations. GUPA
And of
course, no critique of AI would be complete without citing John Searle’s Chinese
Room Argument. Presented in 1980, Searle critiques the notion of
"strong AI" - the idea that computers can genuinely understand and
think like humans. He argues that while machines manipulate symbols using
pre-defined or learned rules, they lack true understanding or consciousness, as
evidenced by a thought experiment in which a person simulates understanding a
language without comprehension. This highlights the distinction between mere
symbol manipulation and genuine semantic understanding. Buffalo
Code
Here’s the full python script: gentext.py