RCS and the Race for Quantum Supremacy: A Practical Look at Benchmarks and Real-World Relevance

 

TL;DR: Google’s Willow chip has smashed its own Random Circuit Sampling (RCS) benchmarks from the 2019 Sycamore system, re-igniting talk about quantum supremacy. But do these record-breaking achievements translate into real-world utility or remain largely symbolic milestones?

 

In this post, we’ll dissect Random Circuit Sampling (RCS) as a benchmark and highlight the ways in which claims of quantum supremacy, particularly Google’s recent announcement, can be misleading without demonstrated real-world applicability. While headlines often tout RCS as proof that quantum processors are surpassing classical supercomputers, it’s critical to understand how RCS works and why it may not directly reflect practical applications. We’ll walk through how RCS experiments are set up, why they’re considered so hard for classical machines, and where these benchmarks do and don’t align with real-world applications. Along the way, we’ll highlight the nature of quantum vs. classical “randomness,” and discuss what these milestones truly mean for the future of quantum computing. By the end, you’ll not only see how RCS generates millions of “bitstrings” in minutes but also appreciate why researchers are still wrestling with the question: is quantum supremacy just around the corner, or do we need more practical tasks to see genuine quantum advantage?

Introduction

Recently, Google announced that its new “Willow” quantum chip surpassed the record-breaking Random Circuit Sampling (RCS) metrics once achieved by the 2019 “Sycamore” system - further amplifying the buzz around quantum supremacy. RCS, in essence, involves running complex, randomly generated quantum circuits on a real device to see if it can produce results faster or more accurately than a classical computer can simulate. The fanfare surrounding these new benchmarks, however, raises an important question: how meaningful is RCS for gauging quantum computing’s readiness for real-world applications?

What is RCS?

Random Circuit Sampling (RCS) involves sampling from the output distribution of a randomly generated quantum circuit, i.e. a random placement of quantum gates, and comparing the empirical distribution to what classical simulation would predict. When the circuit depth and qubit count exceed the classical computability threshold, it can serve as an empirical demonstration of quantum supremacy.

The Issues with the RCS Benchmark

Despite the hype, there’s a lot that can be criticised about the whole RCS benchmark being used to demonstrate quantum supremacy:

  1. Non-verifiability for large circuits
  2. Limited practical utility
  3. Intentionally “unfair” setup
  4. Sensitivity to hardware noise
  5. Near-impossibility of targeted error correction
  6. Difficult interpretation of “Quantum Supremacy”
  7. Media hype and miscommunication

In short, while RCS is an important stress test and a marquee demonstration for quantum hardware capability, it comes with intrinsic caveats around verification, real-world utility, and fairness that limit its broader significance.

However, let’s remain positive and not overly critical; let’s move onto looking at how the experiment is constructed so that we can seek to reproduce it albeit at a much smaller scale…

Experimental Process Flow

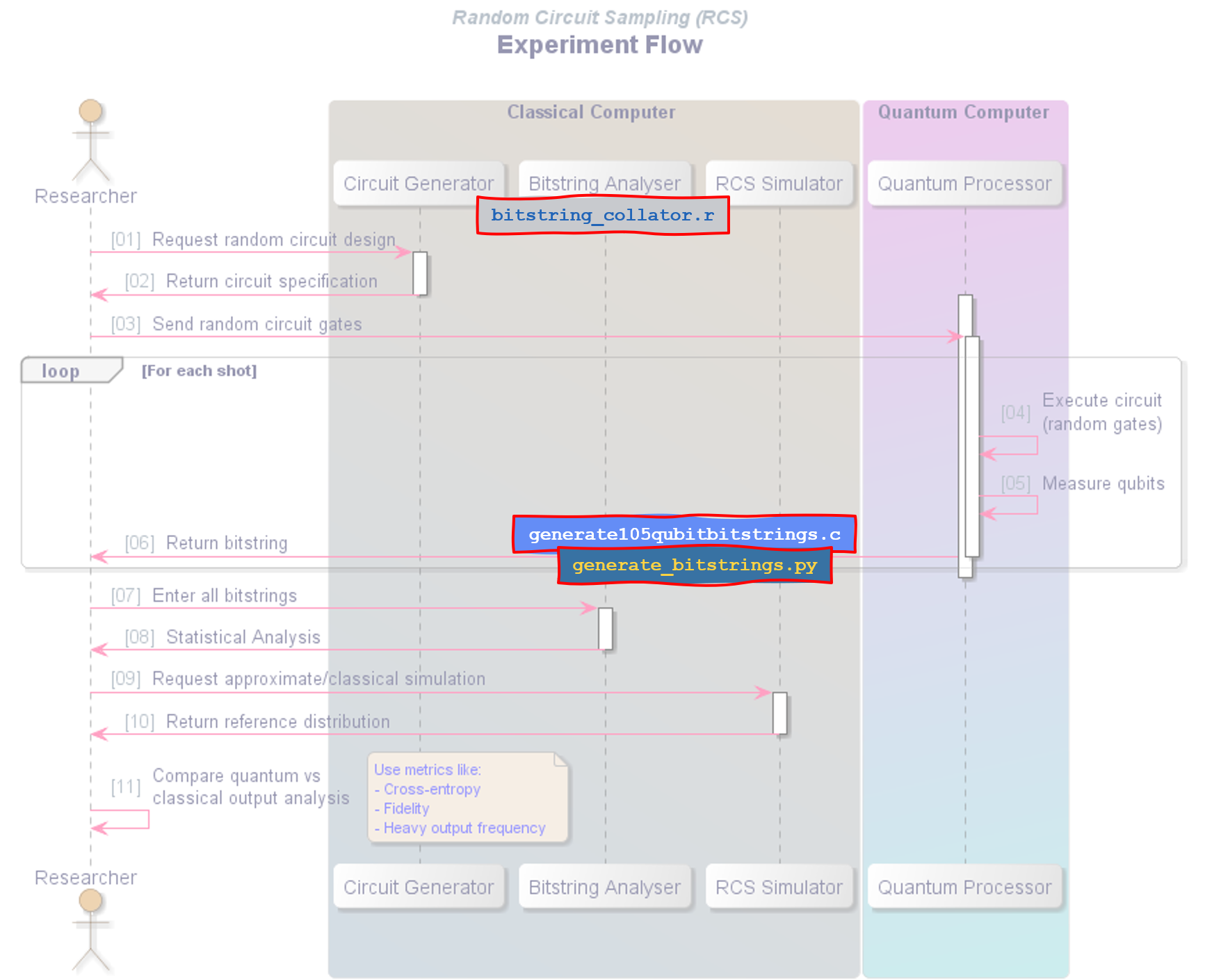
Below is a simplified sequence flow diagram illustrating an RCS experiment. In an actual research or industrial setting, each of these steps could involve far more complexity - multiple layers of error correction, control systems, and in-depth post-processing. However, for educational purposes, this high-level view helps clarify the core responsibilities: how a random circuit is generated and sent to the quantum computer, how the qubits are measured repeatedly (each measurement yielding a bitstring), and how classical analysis then compares the quantum outputs against a reference distribution. This streamlined sequence is a handy reference for understanding the basic workflow behind RCS, without the overhead of real-world engineering details.

 

The process begins when the Researcher requests a random circuit design from the Circuit Generator running on a conventional (classical) computer. Once that specification is returned, the Researcher sends these circuit instructions to the Quantum Processor. The Quantum Processor then executes the specified random gates on its qubits for each shot, measures the resulting bitstring, and returns these bitstrings back to the Researcher. This loop of “execute → measure → return bitstring” continues until sufficient shots have been run to build up a meaningful output distribution.

Back on the classical side, the Researcher sends these bitstrings to the Bitstring Analyser, which performs statistical checks - counting how often each bitstring appears and detecting patterns or “heavy outputs”. In parallel, the Researcher asks the RCS Simulator for a reference distribution, but since a full classical simulation is typically feasible only for small circuits, it may be an approximation.

Finally, the Researcher compares the measured quantum distribution against the classical reference, using metrics like cross-entropy, fidelity, or heavy-output frequency. This comparison step helps validate whether the quantum device’s results align with the idealized model of the circuit, providing insight into both the quantum hardware’s performance and the challenge of simulating it on classical machines.

Our Toy RCS Experiment: From Random Bitstrings to Mock Distribution Analysis

Below you’ll see our RCS process flow diagram again, but this time with our custom scripts overlaid on the relevant steps. This illustrates how we move from Python scripts that generate simplistic random bitstrings, through the C program (generate105qubitbitstrings.c) which creates a more “quantum-like” output at Step 6, to the R script that collates all returned bitstrings and builds a histogram of their frequencies. By matching each program to the appropriate stage in the sequence (e.g., circuit generation, repeated measurement, and final statistical analysis), we replicate key elements of an RCS experiment - even if our toy examples can’t come anywhere close to the complexity of real quantum hardware or the reference classical simulator.

 

Purely Random Bitstring Generation

This Python script below is about as straightforward as it gets: it takes two arguments - “num_qubits” (the length of each bitstring) and “num_shots” (the total number of bitstrings to generate). Then it simply loops “num_shots” times, each time printing out a randomly generated string of 0s and 1s. Although it’s dubbed “naive,” it’s a perfect baseline demonstration for how raw bitstring sampling might look in an RCS-style experiment - except it’s purely uniform random and has no correlation between qubits or shots. Running it with large arguments can produce massive files, as we’ll see below.

def main():

    parser = argparse.ArgumentParser(

        description="Generate random bitstrings given number of qubits and shots."

    )

    parser.add_argument("num_qubits", type=int, help="Number of qubits (bitstring length)")

    parser.add_argument("num_shots", type=int, help="Number of bitstrings to generate")

    args = parser.parse_args()

 

    num_qubits = args.num_qubits

    num_shots = args.num_shots

 

    for _ in range(num_shots):

        # Generate a random bitstring of length 'num_qubits'

        bits = ''.join(str(random.randint(0, 1)) for _ in range(num_qubits))

        print(bits)

 

 

Here, we ran the script with 105 qubits and 18.9 million shots to replicate the data output of Google’s Willow experiment, in size at least. The command took just over 34 minutes of real time, though the “user” and “sys” times are minimal because the process is mostly waiting on I/O. Willow produced this quantity of data in under 5 minutes.

 

07:39:40 User@AN20 ~/QuantumBenchmark 980 0 😊 $ time ./generate_bitstrings.py 105 18900000 > 105qubit_bitstrings.txt

 

real    34m41.455s

user    0m0.046s

sys     0m0.061s

 

Finally, to confirm, we see that “wc -l” reports exactly 18,900,000 lines in the output, each line being a 105-bit string, yielding a total file size of roughly 1.9 GB. This not only indicates we successfully generated the intended number of bitstrings, but also highlights how quickly these experiments can produce huge datasets. In a real RCS experiment, the quantum machine’s measurement shots can likewise accumulate staggering amounts of output data, though the distribution (and hence the challenge in reproducing it classically) is often far more complex.

08:16:58 User@AN20 ~/QuantumBenchmark 218 0 😊 $ wc -l 105qubit_bitstrings.txt

18900000 105qubit_bitstrings.txt

08:36:59 User@AN20 ~/QuantumBenchmark 419 0 😊 $ du -h 105qubit_bitstrings.txt

1.9G    105qubit_bitstrings.txt

 

Bitstring Analysis

The following R script (bitstring_collator.r) demonstrates a simple approach to reading a large text file of bitstrings, computing the frequency of each unique string, and visualizing the results. It’s designed to handle millions of lines, though as we’ll see, memory usage can grow quickly if each bitstring is unique (as in a purely random dataset). The script also produces basic statistics - like how many total shots were recorded, how many distinct bitstrings were found, and the top five most frequent bitstrings - before plotting a histogram (in probability form).

# Parse Command-Line Argument(s)

args <- commandArgs(trailingOnly = TRUE)

if (length(args) < 1) {

  stop("Usage: Rscript bitstring_collator.R <bitstrings.txt file>")

}

bitstring_file <- args[1]

 

# Read Bitstring Data

bitstrings <- readLines(bitstring_file)

cat(

    "Size of 'bitstrings' object:",

    format(object.size(bitstrings), units = "auto"), "\n"

)

 

# Calculate Frequencies

freq_table <- table(bitstrings) # table() gives you counts of each unique bitstring

df_freq <- as.data.frame(freq_table) # convert table to data frame

colnames(df_freq) <- c("bitstring", "count")

 

# Compute Probabilities

df_freq$prob <- df_freq$count / sum(df_freq$count)

 

# Print Basic Stats

cat("Total Shots:", sum(df_freq$count), "\n")

cat("Unique Bitstrings:", nrow(df_freq), "\n\n")

 

# Show the top 5 most common bitstrings

df_freq_sorted <- df_freq[order(-df_freq$count),]

cat("Top 5 Most Frequent Bitstrings:\n")

print(head(df_freq_sorted, 5))

 

# Plot Histogram of counts or probabilities

suppressPackageStartupMessages(library(ggplot2))

p <- ggplot(df_freq, aes(x = bitstring, y = prob)) +

    geom_bar(stat = "identity", fill = "steelblue") +

    labs(

        title = "Histogram of Measured Bitstrings",

        x = "Bitstring",

        y = "Probability"

    ) +

    theme_minimal()

 

# Save the Plot

output_file <- gsub("\\.bits$", ".histogram.png", bitstring_file)

cat("Saving histogram to", output_file, "\n\n")

ggsave(output_file, p, width = 16, height = 9)

 

By running bitstring_collator.r on our massive 18.9 million line file of 105-qubit bitstrings, we quickly see the practical impacts of storing so many unique strings in memory. The script reports 3.2 GB of memory usage just to load the dataset - reflecting the fact that each 105-bit string is stored as a long character vector in R. We also observe that every shot is unique (18.9 million unique strings), confirming that the purely random generator had zero collisions. The script was interrupted before it attempted to draw the histogram - it would have “flat-lined” at y=1 for 18.9 million values of x.

08:17:08 User@AN20 ~/QuantumBenchmark 228 0 😊 $ time ./bitstring_collator.R 105qubit_bitstrings.txt

Size of 'bitstrings' object: 3.2 Gb

Total Shots: 18900000

Unique Bitstrings: 18900000

 

real    18m50.782s

user    0m0.000s

sys     0m0.046s

 

The Vastness of the State Space

To get a sense of scale, 2105 is approximately 4.03×1031 - that’s a 4 followed by 31 zeros. Put another way, there are more possible states in 105 qubits than there are stars in the observable universe by many orders of magnitude. This is why even 18.9 million samples barely scratches the surface of such an enormous space, and why collisions are so unlikely when the distribution is nearly uniform.

And to get a rough sense of how many times we would have to produce 18.9 million 105-bit strings before expecting even one collision, we can invoke the birthday paradox. In a uniform distribution of size 2105, the expected number of draws needed for a ~50% chance of collision is on the order of:

$$ \sqrt{2^{105}} = 2^{\frac{105}{2}} \approx 2^{52.5} \approx 6.4 \times 10^{15} $$

Each block of 18.9 million (1.89×107) bitstrings is one “batch” of draws. So, the number of batches needed for an expected collision is roughly:

$$ \frac{6.4 \times 10^{15}}{1.89 \times 10^7} \approx 3.4 \times 10^8 \approx 340 \text{ million} $$

Putting That in Perspective

$$ 3.4 \times 10^8 \times 1.89 \times 10^7 \approx 6.4 \times 10^{15} $$

$$ 3.4 \times 10^8 \times 1.9GB \approx 6.5 \times 10^8 GB \approx 650PB $$

This is why, in purely uniform sampling of 105-bit outputs, collisions are basically never observed for any realistic number of shots. In the next example, when we introduce skew or “heavy” outputs, we’ll see how this same R script can reveal drastically different patterns of repetition and collisions.

Beyond Uniform Randomness: A Toy RCS Generator in C

After experimenting with our naive Python bitstring generator, we learned two important lessons:

  1. Pure uniform randomness across 105-bit strings leads to virtually no collisions in tens of millions of samples, making it a poor analogue for real RCS outcomes.
  2. Handling data at scale - both in memory and I/O - can become a major bottleneck if every bit is naively stored as an entire character.

To address these points, we turn to a C-based approach. First, we introduce non-uniform distributions (log-normal amplitudes) to ensure some “heavy” bitstrings appear more often. Second, we store each 105-bit pattern in 14 bytes rather than the earlier 105 bytes, packing bits and avoiding the inefficiency of strings. The resulting program still can’t replicate the full complexity of a quantum circuit’s output, but it produces a more skewed distribution - helping us see collisions, large-scale repetition, and other phenomena reminiscent of real RCS experiments.

Here are some key snippets from the program:

Th Box–Muller transform function draws two uniform [0,1] samples (u1, u2) and converts them to a Gaussian (μ=0, σ=1) random number. The program uses this to create a log-normal amplitude later, which helps shape the distribution of output strings so some appear more frequently - mimicking a skewed, RCS-like distribution.

static double rand_normal()

{

    double u1 = (double)rand() / (double)RAND_MAX;

    double u2 = (double)rand() / (double)RAND_MAX;

    double r = sqrt(-2.0 * log(u1));

    double theta = 2.0 * M_PI * u2;

    double z = r * cos(theta); // normal(0,1)

    return z;

}

 

The following code assigns a log-normal amplitude to each pattern. The squaring that amplitude makes the distribution even more skewed, so a small fraction of patterns end up with disproportionately high probability. It then cumulatively sums these weights and normalizes them, building a Cumulative Distribution Function (CDF).

    for (int i = 0; i < subset_size; i++)

    {

        double z = rand_normal();         // normal(0,1)

        double amplitude = exp(z);        // log-normal(0,1), a positive value

        double w = amplitude * amplitude; // square for a more pronounced weight

        weights[i] = w;

    }

…

    for (int i = 0; i < subset_size; i++)

    {

        running += weights[i];

        cdf[i] = running / sum_w; // normalized

    }

 

By sampling from this CDF, the program enforces that high-weight patterns appear more often in the final output file - similar to how some bitstrings in an RCS experiment can have a higher amplitude (and thus higher probability).

Each shot picks a random double r ∈ [0,1] and searches the CDF to find which pattern’s probability range it falls into. This binary search makes lookups O(log n) rather than O(n) - important if subset_size is large.

static int find_index_in_cdf(const double *cdf, int size, double r)

{

    int left = 0;

    int right = size - 1;

 

    while (left < right)

    {

        int mid = (left + right) / 2;

        if (cdf[mid] < r)

        {

            left = mid + 1;

        }

        else

        {

            right = mid;

        }

    }

 

    return left; // left == right => the position

}

 

Together, these snippets show how the C program creates a nonuniform, skewed distribution of 105-bit strings. It’s just a toy version of “random circuit sampling” - instead of deriving probabilities from an actual quantum circuit, it uses log-normal weights to produce “heavy outputs.” The goal is to generate collisions and an uneven histogram that’s a bit more representative of realistic (but still vastly simplified) quantum RCS outputs.

Here is the compiled C program being run with a subset size of 10,000 and our usual 18.9 million shots (in keeping with the Willow experiment) followed by the bitstring_collator.r script:

06:28:21 User@AN20 ~/QuantumBenchmark 101 0 😊 $ time ./generate105qubitbitstrings.exe 10000 18900000 105qubit_lognormal_bitstrings.txt

 

real    3m10.805s

user    3m6.796s

sys     0m0.859s

07:37:30 User@AN20 ~/QuantumBenchmark 250 0 😊 $ time ./bitstring_collator.R 105qubit_lognormal_bitstrings.txt

Size of 'bitstrings' object: 145.9 Mb

Total Shots: 18900000

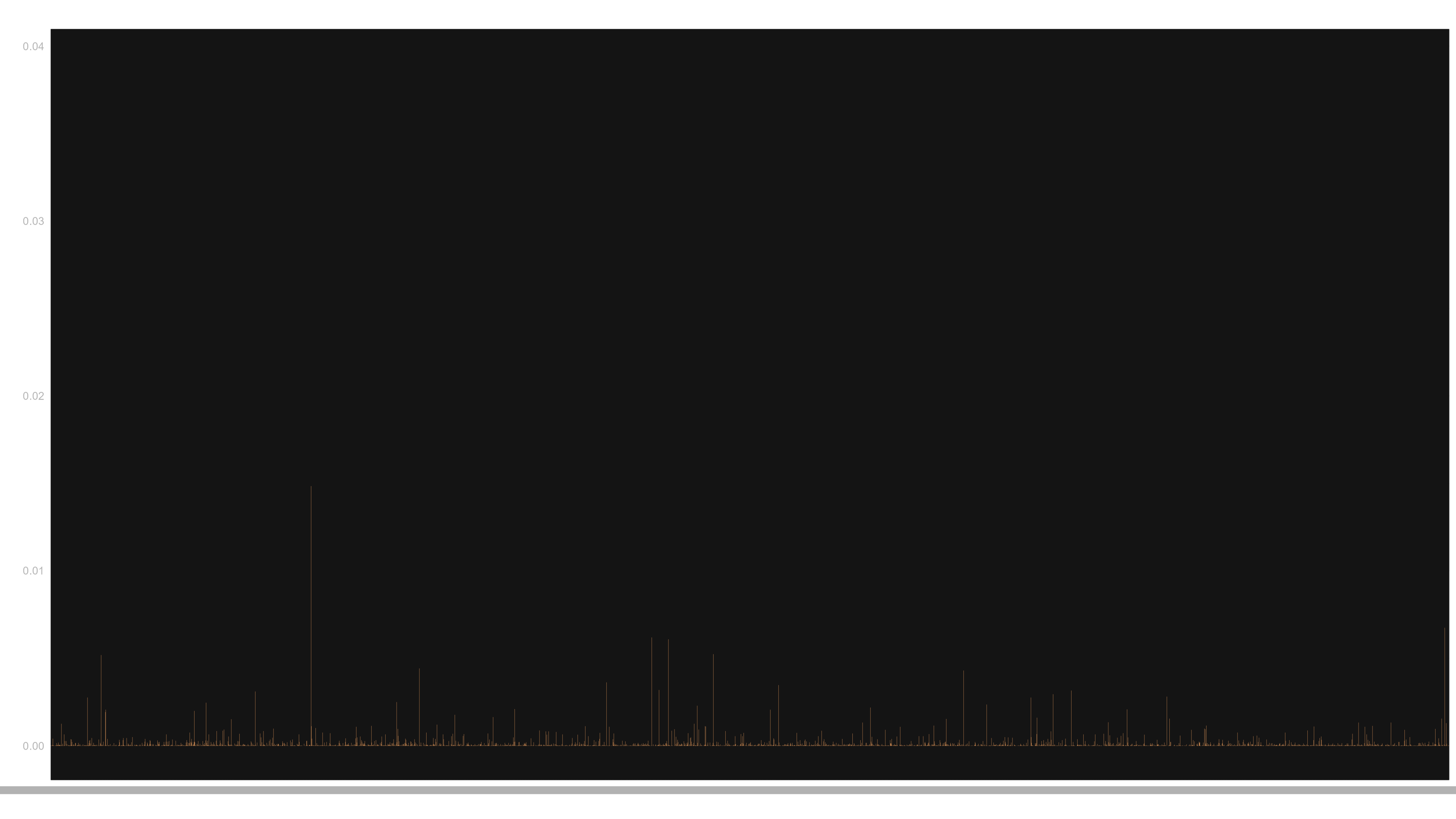
Unique Bitstrings: 9955

 

Top 5 Most Frequent Bitstrings:

                                                                                                     bitstring

7865 110010000000111001001001000110110101011110000101000111110100101000100011111001011001010000001010100011000

5343 100001110010000101101010010001011011100001010001110100010010110011001111010111101101000010101000110011000

1854 001011110000001100101000110111000010000001000011001110110010110100101111010010010111110001100000101110011

3337 010101000101001101111111010101001000000011011111011110100110101110100110111001111111110010100001001100001

503  000011001101001110001111011101101001101001001110011110010001000001100101111010101101100010001000101001111

      count        prob

7865 737499 0.039021111

5343 371077 0.019633704

1854 280379 0.014834868

3337 204757 0.010833704

503  170701 0.009031799

 

real    0m25.798s

user    0m0.000s

sys     0m0.015s

 

Notice several important differences compared to the Python scenario:

  1. Faster Generation
  2. Memory and Collisions
  3. Representative “Heavy Outputs”

Overall, this more realistic (though still toy) approach illustrates how skew in the distribution can force actual repetition and a “heavy-tail” effect - vaguely mirroring the kind of output that might arise from an actual Random Circuit Sampling experiment on quantum hardware.

Finally, here is the histogram generated by the R script:

 

Conclusion

In this article, we replicated the basic flow of a Random Circuit Sampling experiment- albeit in a toy fashion. We showed how uniform random bitstrings fail to capture any real collisions and how a lognormal-based approach in C yields a more skewed distribution that hints at the kind of “heavy outputs” often reported in true RCS studies. By using Python for naive generation, a C program for more nuanced sampling, and R for collation and histogram analysis, we illustrated several key lessons:

The [F]utility of RCS Benchmarking

Yet, it’s important to recognize the limitations of RCS itself. The benchmark is intentionally designed to be hard for classical computers but more “natural” for quantum devices. In this sense, it serves as a theoretical stress test rather than a practical solution to a real-world computational need. Some argue that this mismatch renders RCS an unfair comparison: it doesn’t address industrial problems like optimization or cryptography, yet it trumpets “supremacy” simply because classical simulation at large scale becomes infeasible.

At the same time, RCS has value as a demonstration of hardware maturity - showing that qubits can generate massive, complex distributions no known classical machine can match. But its “[f]utility” lies in the fact that, while it makes for a bold headline, it doesn’t immediately translate into breakthroughs in commercial or scientific fields. Instead, RCS is a niche benchmark that leverages quantum effects in a contrived setting, making it a spectacular but ultimately futile show of power.

What’s Next

Looking ahead, we’ll push beyond purely synthetic datasets. In our next post, we’ll generate actual random quantum circuits, run them on a small, real quantum processor, and compare those outputs against a well-established classical simulator. Naturally, we’re limited to only a few qubits, as large-scale classical simulation remains out of reach for everyone - even Google. Still, it’s a vital step toward understanding the true nature of quantum supremacy claims: not only how quantum devices handle contrived tasks, but also whether these insights hint at future, genuinely useful quantum applications.

 


[1] Numbers based on publicly available data as of December 2024, typically calculated by the claimed content added daily and earlier trends.