The Quantum Frontier: Revolutionizing Cryptography with Quantum Computers

TL;DR: The rise of quantum computing threatens traditional cryptographic methods. However, quantum mechanics also provides a solution: quantum cryptography with protocols such as BB84 that enable the exchange of encryption keys in a way that is immune to eavesdropping.

Introduction

As digital security faces unprecedented challenges with the rise of quantum computing, the field of cryptography stands at a crossroads. Traditional public-key cryptographic systems, while reliable today, will soon be rendered obsolete by the computational power of quantum computers. However, the principles of quantum mechanics not only expose these vulnerabilities but also offer solutions, paving the way for the next generation of secure communication.

In this exploration, we’ll trace the evolution of cryptography - from the foundation of public-key systems to the advent of quantum cryptography and Quantum Key Distribution (QKD). Along the way, we’ll uncover how quantum phenomena like superposition, entanglement, and the no-cloning theorem are revolutionizing how we protect information in a rapidly advancing digital world.

Public Key Cryptography

To explain public key cryptography, it is instructive to first look at the traditional way messages are encrypted and decrypted between two people (or systems). That is, by using a key known to both parties. This is known as a symmetric key system as illustrated below…

As should be apparent, this method relies on the sharing of a private key. However, the key must be securely exchanged beforehand, leaving it vulnerable to interception by eavesdroppers.

The public key system uses an asymmetric key method, i.e., different keys are used to encrypt and decrypt, one of which is made public and the other kept private. This public-private key pair is generated using a one-way mathematical function - calculations that are easy to perform but infeasible to reverse without specific information. For example, the widely used RSA algorithm (Rivest, 1978) leverages the difficulty of factoring large numbers into primes. While multiplying two large primes is straightforward, deducing the original primes from their product is computationally prohibitive.

The public key can be shared with the world and anyone wishing to send you a secret message can use this to encrypt it, as illustrated below…

The RSA algorithm requires several computationally expensive operations, so it is often used to send a short-term symmetric key. The actual message can then be quickly encrypted and decrypted using this symmetric key.

Quantum Computers

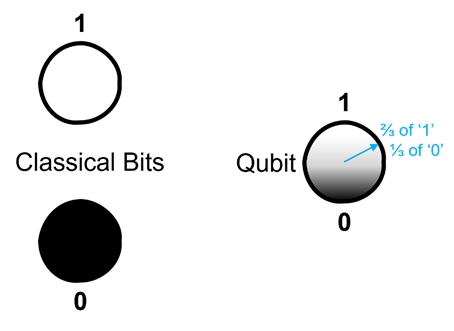
Quantum computers represent a groundbreaking shift from classical computing. While classical computers store and process data in binary digits (bits), quantum computers use quantum bits, or qubits. Qubits leverage quantum phenomena such as superposition (often illustrated with the thought experiment, “Schrödinger's cat”), allowing them to represent both 0 and 1 simultaneously, as illustrated below…

This ability to exist in multiple states at once enables quantum computers to perform many calculations in parallel. Entanglement, another quantum phenomenon, further amplifies this power. When qubits are entangled, measuring the state of one instantaneously determines the state of the others, regardless of their physical distance. Together, superposition and entanglement allow quantum systems to solve problems exponentially faster than classical ones.

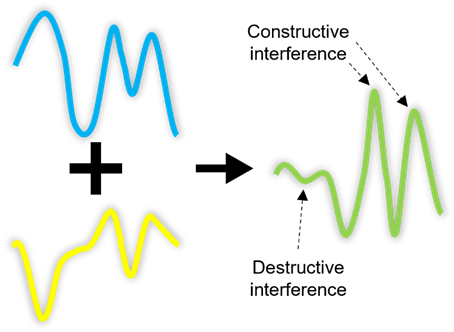
Finally, as qubits are probabilistic, they can be modelled as waves and multiple qubits can interfere with each other. This interference results in combined waves with amplitudes changed as illustrated below…

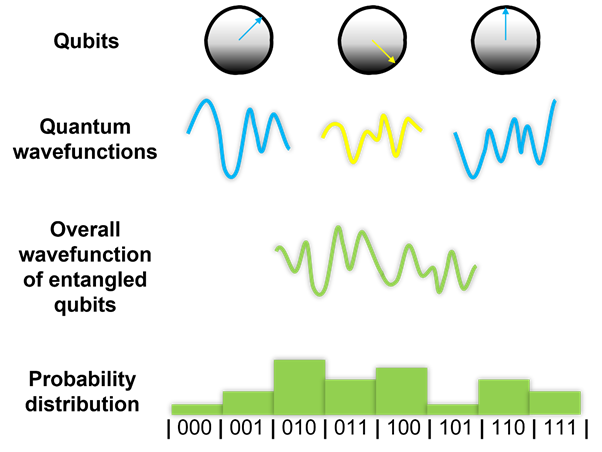
The next diagram shows three entangled qubits with their overall wavefunction and the resulting probability distribution. A quantum circuit would produce all the outputs at once and a measurement can identify the correct answer.

The more qubits that are entangled together, the greater the number of simultaneous states…

Number of qubits	1	2	3	4	…	20	…	n
Number of states	2	4	8	16	…	1,048,576	…	2^n

Shor's algorithm (1995) demonstrates how a quantum computer can efficiently factorize large numbers - a task so computationally intensive on classical machines that it forms the foundation of public-key encryption. The graph below shows the comparison between Shor’s algorithm versus the best classical algorithm that takes thousands of CPU years to factorise a 230-digit number…

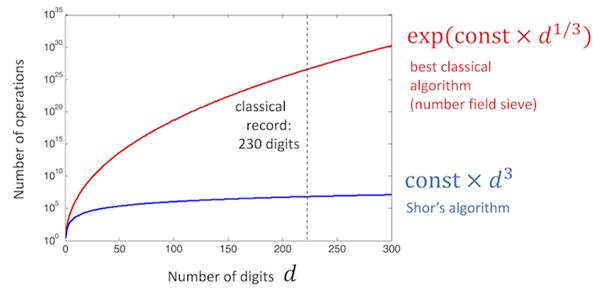
(Image courtesy of IBM: Cross)

However, building practical quantum computers remains challenging. Large-scale systems with 1000+ qubits are needed to break current encryption, but issues like qubit stability and error correction must first be overcome.

Quantum Cryptography

As quantum computers threaten the security of existing cryptographic methods, quantum cryptography offers a revolutionary alternative. By leveraging the principles of quantum mechanics, it ensures that messages can be encrypted in a way that is immune to eavesdropping and cannot be intercepted without detection.

Traditional cryptographic systems rely on one-way mathematical functions that are computationally difficult to reverse. However, quantum computers, with their ability to perform calculations in parallel, can solve these problems in polynomial time, rendering current public-key encryption methods insecure. Additionally, public keys depend on certificate authorities for authentication, which are vulnerable to breaches or insider threats.

Quantum cryptography addresses these vulnerabilities through the unique properties of quantum mechanics:

· Heisenberg Uncertainty Principle: Certain physical properties of quantum particles cannot be simultaneously known, ensuring security during measurement.

· Superposition: Quantum entities exist in multiple states at once, allowing secure encoding.

· Measurement Paradox: Any attempt to measure a quantum system disturbs it, making eavesdropping detectable.

· No-cloning Theorem: Quantum states cannot be perfectly duplicated, preventing replication of secure keys.

These principles enable methods like Quantum Key Distribution (QKD) to securely establish encryption keys. The following table illustrates how quantum computers impact traditional cryptographic algorithms and underscores the need for quantum-secure alternatives…

Cryptographic Algorithm	Type	Purpose	Impact from large-scale quantum computer
AES	Symmetric key	Encryption	Larger key needed
SHA-2, SHA-3	n/a	Hash functions	Larger output needed
RSA	Public key	Signatures, key establishment	No longer secure
ECDSA, ECDH (Elliptic Curve Cryptography)	Public key	Signatures, key exchange	No longer secure
DSA (Finite Field Cryptography)	Public key	Signatures, key exchange	No longer secure

As quantum technology progresses, quantum cryptography is poised to become the foundation of secure communication in a quantum-powered world.

Quantum Key Distribution (QKD)

An important property of the quantum world (a corollary of the no-cloning theorem) is the impossibility to discriminate two non-orthogonal states reliably. So, if a photon has been polarised in the horizontal-vertical (rectilinear) plane or diagonally, a measurement cannot be made to distinguish between all four states. Additionally, the fact that measurements disturb quantum states (the measurement paradox), prevents repeated measurements using one basis followed by another.

Charles Bennet and Gilles Brassard exploited these phenomena when they proposed, what has since been called, the BB84 protocol (Bennet, 1984). Alice, being the sender, deploys a BB84 transmitter while Bob has a BB84 receiver…

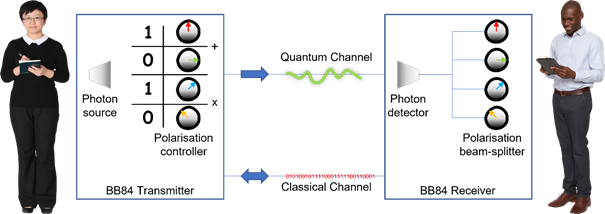
A scheme for relating polarisation of a photon to a bit value is agreed: in this case we have 1 for vertical and +45° and a 0 for horizontal and -45°.

Alice creates a random bitstream and an equal length of random choices for the polarisation basis (rectilinear or diagonal). The BB84 transmitter takes these two inputs to generate a sequence of polarised photons which are then sent over the quantum channel. Bob, independently and randomly, chooses the polarisation bases for the photons he receives and calculates the values of bits…

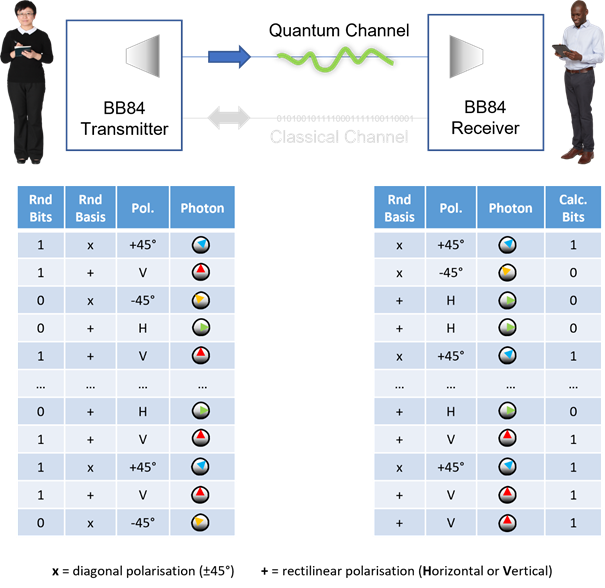
Next, Alice sends the list of bases to Bob over the clear classical channel. Bob can discard all values where his basis selection differed…

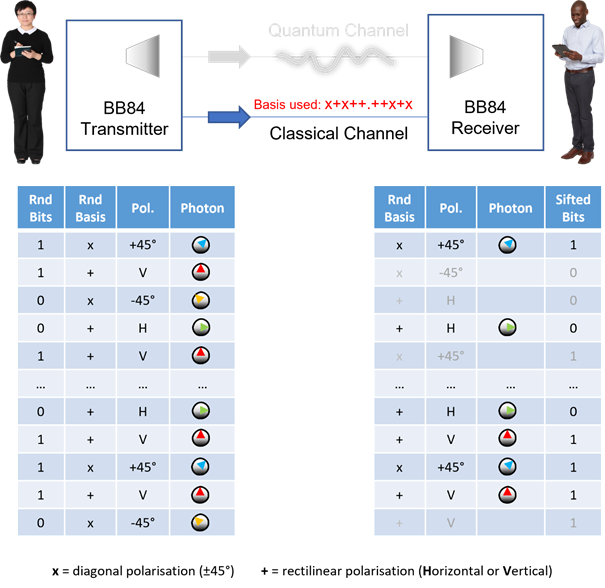
Bob does the same and Alice discards the non-matching basis bits…

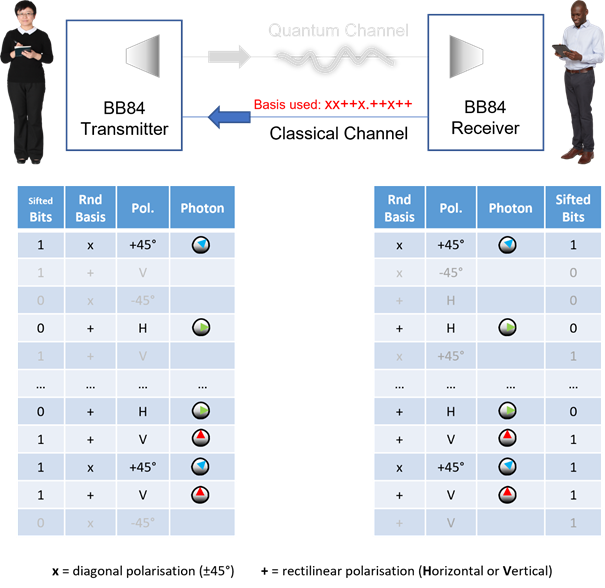
What remains is a set of bits that are equal for both, and this is now their symmetric session key for encrypting data over the classical channel.

QKD’s quantum principles ensure that any eavesdropping attempt disrupts the photon states, alerting Alice and Bob to potential interference. This makes QKD fundamentally secure against interception.

While QKD has traditionally been limited by distance, advancements such as entangled photon sources and high-quality fibre optics have extended its range significantly. For instance, recent experiments have achieved secure key distribution over hundreds of kilometres, paving the way for large-scale quantum-secure networks.

References

Bacco, D. et al (2021) “A proposal for practical multidimensional quantum networks”. Vienna University of Technology: Atomic Institute. Available at https://arxiv.org/pdf/2103.09202v2

Bennett, Charles H., and Brassard, Gilles (1984) “Quantum Cryptography: Public Key Distribution and Coin Tossing.” Theoretical Computer Science, vol. 560, Dec. 2014, pp. 7–11. Available at https://doi.org/10.1016/j.tcs.2014.05.025

Chen L, Yi-Kai L, Jordan S, et al. (2016) “Report on Post-Quantum Cryptography (NISTIR 8105)”. National Institute of Standards and Technology. Available at http://nvlpubs.nist.gov/nistpubs/ir/2016/NIST.IR.8105.pdf

Cross, Abby (editor) (year unknown) “Shor’s Algorithm”. IBM Quantum Composer User Guide. Available at https://quantum-computing.ibm.com/composer/docs/iqx/guide/shors-algorithm

Korolov, M., Drinkwater, D. (2019) “What is quantum cryptography? It’s no silver bullet, but could improve security”. CSO (UK). Available at https://www.csoonline.com/article/3235970/what-is-quantum-cryptography-it-s-no-silver-bullet-but-could-improve-security.html

Martín-López, E., Laing, A., Lawson, T. et al. Experimental realization of Shor's quantum factoring algorithm using qubit recycling. Nature Photon 6, 773–776 (2012). Available at https://doi.org/10.1038/nphoton.2012.259

Shor, P.W. (1994). "Algorithms for quantum computation: discrete logarithms and factoring". Proceedings 35th Annual Symposium on Foundations of Computer Science. IEEE Comput. Soc. Press: 124–134. Available at https://doi.org/10.1109%2Fsfcs.1994.365700

USTC (2021) “The world's First Integrated Quantum Communication Network”. University of Science and Technology of China. Available at https://en.ustc.edu.cn/info/1110/4016.htm

Wang, S., Yin, ZQ., He, DY. et al. (2022) “Twin-field quantum key distribution over 830-km fibre”. Nature Photonics 16, 154–161. Available at https://doi.org/10.1038/s41566-021-00928-2

Weier, Henning (2003) “Experimental Quantum Cryptography”. Ludwig-Maximilians-University Munich. Available at https://xqp.physik.uni-muenchen.de/publications/theses_diplom/diplom_weier.html

Bibliography

Buchanan, William & Woodward, Alan (2016) “Will quantum computers be the end of public key encryption?” Journal of Cyber Security Technology. 1. 1-22. 10.1080/23742917.2016.1226650. Available at https://www.tandfonline.com/doi/pdf/10.1080/23742917.2016.1226650

Microsoft (n.d.). “What is a qubit?”. Available at: https://azure.microsoft.com/en-us/overview/what-is-a-qubit/

Tabb, Michael, Gawrylewski, Andrea and DelViscio, Jeffery (2021). “How Does a Quantum Computer Work?”. Available at:https://www.scientificamerican.com/video/how-does-a-quantum-computer-work/

Weier, Henning (2003) “Experimental Quantum Cryptography”. Ludwig-Maximilians-University Munich. Available at https://xqp.physik.uni-muenchen.de/publications/theses_diplom/diplom_weier.html