Scheduling Fair Play: The Circle Method & CORRA Foundations

 

TL;DR: Beneath every round-robin lies an NP-hard puzzle of pairings, courts, and timing. CORRA (ClubOps Round-Robin Americano) solves it heuristically – generating full-season schedules with near-perfect fairness, instantly adaptable to real-world constraints and last-minute changes in the blink of an eye.

 

 

1.  The Problem with “Simple” Fairness

Let’s start with something familiar. Imagine a tennis or pickleball club with twenty regular players and a few guests. The group plays twice a week over a season lasting several months. Everyone wants the same things: a balanced mix of partners, a wide range of opponents, and as few idle rounds as possible. The organisers would also like to keep a leaderboard and finish the season with prizes.

On paper that sounds trivial – just rotate the names and go! In practice, one player forgets to confirm attendance, another is injured, a court is flooded (damn that leaky roof), and the lights must go out at nine o’clock. Suddenly “fair scheduling” becomes a puzzle.

This post introduces CORRA – the ClubOps Round-Robin Americano engine, a scheduler designed to preserve fairness even when real life interferes. It builds on century-old geometric ideas, adds modern optimisation theory, and delivers fast, adaptive match lists that feel human rather than mechanical.

2.  The Circle Method – Fairness through Geometry

Long before computers, tournament organisers used a beautifully simple technique for round-robins: the circle method. Write all team names around a circle, fix one at the top, and rotate the rest clockwise each round. Each rotation defines a new set of pairings.

For an even number of teams, one position is anchored; for an odd number, one slot becomes a bye. The result guarantees that every team meets every other team exactly once, with balanced home/away symmetry.

 

 

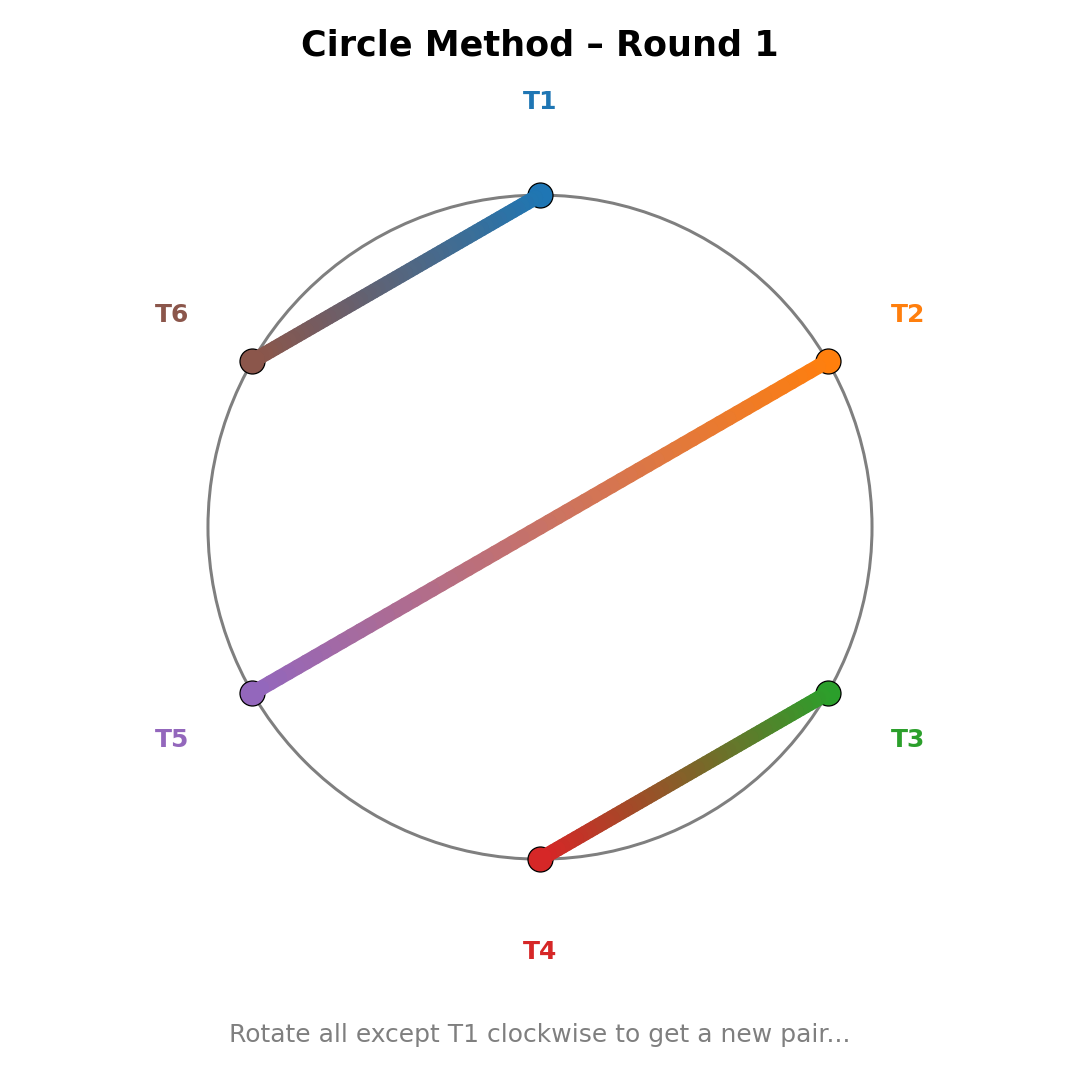
Play with the Circle Visualiser (EPL 20-Team Edition)

The Circle Method demonstrates several key scheduling principles:

Circle Behaviour

Scheduling Principle

Fixed top node

Anchoring constraint

Clockwise rotation

Systematic variation

Opposite pairing

Uniform coverage

Half-circle symmetry

Equal home/away balance

Complete rotation

Exhaustive fairness

 

The method’s elegance lies in its geometry: fairness emerges from rotation, not calculation. Yet its beauty fades when reality intrudes – because geometry assumes perfection.

3.  From Circle to Complexity – When Fairness Meets Reality

If you’ve ever wondered why the English Premier League fixture list takes weeks to publish, it’s not laziness. The league starts with a perfect circle-method template – each of the twenty teams plays the other nineteen twice. But then the real-world constraints arrive: no more than two consecutive home matches, derbies kept apart for crowd control, television slot balancing, travel limits, and even local events like city marathons.

Here's what all this complexity looks like as a state transition diagram:

 

At a smaller scale, your local racquet club faces the same chaos. You may not worry about police logistics, but you must juggle unavailable courts, uneven attendance, and the desire for variety and rest balance. Each extra rule twists the elegant circle into a web of dependencies.

 

Complexity Theory: The Scale of the Search Space

Even a simple singles round-robin is combinatorially explosive. A single session is a perfect matching of the complete graph KN, counted by the odd double factorial (N – 1)‼
For 20 players, that’s a lot of distinct pairings in just one session:

(19)‼ = 654,729,075 ≈ 6.55 x 108

A full 19-session season would therefore have roughly 10167 possible arrangements:

((19)‼)19 ≈ 10167

For doubles, the count is even worse: (20! / (4!)55!) x 35 ≈ 6 x 1011 per round, or about 10224 over 19 sessions.

These aren’t approximations – they’re exact combinatorial counts, and they illustrate why exhaustive enumeration is impossible in practice. Every added constraint (courts, fairness, repeat limits) narrows the feasible set but makes the search landscape vastly more complex. In other words, the search space becomes smaller in size but more tangled in shape with every added dimension. This results in perfect and complete searches being even more intractable than the astronomical numbers above as the algorithm would lead to many dead ends (infeasible selections as per the constraints) and necessarily backtrack.

 

4.  The NP-Hard Heart of Fair Scheduling

Formally, the moment you add fairness and court limits, the scheduling problem becomes a member of the NP-hard family. For singles, choosing rounds under a limited number of courts is equivalent to a capacity-constrained edge-colouring of Kn, shown by Holyer (1981) to be NP-complete. For doubles, minimising repeat partners or opponents generalises the Social Golfer Problem, also NP-complete.

 

NP-Hard Family Members

Problem Type

CORRA Analogy

Computational Class

Graph colouring

Assigning partners without repetition

NP-complete

Steiner system design

Ensuring every subset occurs once

NP-hard

Balanced incomplete block design

Even opponent distribution

NP-hard

Social Golfer Problem

Every player meets every other

NP-hard

 

 

In plain English: even deciding whether a perfect schedule exists can take more time than the universe has left to compute it. The following tables show this combinatorial explosion:

Players
N

Unique pairings
N(N-1)/2

Complete rounds
(N-1)‼

Full round-robin orders (N-1)!

6

15

15

120

8

28

105

5,040

10

45

945

362,880

12

66

10,395

39,916,800

14

91

135,135

6,227,020,800

16

120

2,027,025

1,307,674,368,000

18

153

34,459,425

355,687,428,096,000

20

190

654,729,075

121,645,100,408,832,000

Players
N

Courts
N/4

Doubles session configurations
(N! /
(4!)N/4(N/4)!) x 3N/4

Naive full-season orders (session configs)N-1

8

2

315

307732862434921875

12

3

155,925

13245650146078617600...................................... (58 digits)

16

4

212,837,625

83315549209501777920......................................................................................................... (125 digits)

20

5

618,718,975,875

10923838769387317248......................................................................................................................................................................................... (225 digits)

 

5.  CORRA’s Approach – From Theory to Practice

Because perfect optimisation is impossible at human timescales, CORRA takes a pragmatic path. It converts an intractable global search into a series of fast, local decisions.

Each schedule can be represented as a three-dimensional tensor (round,court,position) mapping player IDs to slots. CORRA builds this tensor greedily, one round at a time, guided by live fairness statistics:

The result: schedules that complete in milliseconds, maintain >95% opponent coverage for a typical season, and gracefully handle mid-session disruptions.

The following diagram shows CORRA’s state transition with the Fairness Heuristic at the heart of the scheduler:

 

 

Heuristics: How CORRA Stays Fast

CORRA sidesteps the combinatorial explosion through greedy local optimisation. In practice, this means: build the current round using well-chosen heuristics, don’t look forward for theoretical perfection, and don’t go back to revise earlier decisions; just pick the current (local) optimum. If the heuristics are good, you’ll stay close to perfection over the long run.

To support those fairness heuristics, CORRA maintains running statistics (partner counts, opponent counts, and “last-played” indices) in hash maps, allowing constant-time, i.e. O(1), lookups for every candidate pairing.

Each round builds matches by scanning O(N2) potential pairs and selecting the best-rated combination based on weighted fairness terms. With C courts and K rounds, total complexity is O(KCN2) – comfortably polynomial, not exponential.

For realistic club-session sizes (under 32 players and half a dozen courts), CORRA completes in milliseconds. Even if you were to pre-prepare the full season’s fixtures all once, it’s still sub-second performance. We’ll explore the specific heuristics and real-world performance benchmarks in the next post.

In short: the algorithm converts an intractable combinatorial search into a deterministic, quadratic-time construction that’s fair (typically obtaining ≈98% coverage over a season), resilient, and immediate.

 

 

Greedy Local Optimisation – The House Move Analogy 🚚

Imagine you’re packing a delivery van with everything from a three-bedroom family home. It is possible to achieve the mathematically perfect packing order, the one that uses every cubic centimetre of space. But you’d have to try billions of permutations: what if the sofa goes first? what if the dining table tilts upright, or at 51.52° to fit that mini Louvre Pyramid you insist on having? what if the boxes stack differently? A computer could spend years evaluating all those options.

Professional movers, though, don’t do that. They glance at the van, judge the shapes and weights, and instinctively pack the next thing that fits best at that moment, leaving things that they know will fit better later to one side. They don’t achieve the absolute theoretical optimum, but the van is full, stable, and done in hours.

That’s what CORRA’s greedy local optimisation does: it doesn’t simulate every possible round for the session or for the whole season. It just keeps making the best next move based on the current state. It fills the schedule efficiently, fairly, and fast so the “van” (your season) is neatly packed long before the brute-force algorithm would even have loaded the first box.

 

6.  Fairness Under Pressure – CORRA in Action

Real sessions rarely stay stable. Players arrive late, miss a session or two, a court goes out of use, or an incident causes a delay. CORRA handles these disruptions gracefully. If a session runs short, it can rebalance its time budget – trimming remaining rounds while preserving opponent coverage. If the venue permits, it can extend the schedule instead.

Over a full season, absences even out. A player missing a week or two will naturally fall behind in match count, but CORRA’s heuristics have a self-correcting bias: underplayed participants are preferentially scheduled until equity is restored. By the final rounds, game counts and opponent coverage are typically balanced again – unless someone has been away for months (in which case, remind them not to miss the last session!).

The result is practical fairness under real-world constraints: a schedule that feels right.

 

Takeaway: Fairness starts with geometry but survives through computation.
The circle method gave us the visual ideal of equality; CORRA extends that ideal into the unpredictable, time-limited world of modern clubs. It doesn’t chase mathematical perfection – it achieves practical fairness, fast.

 

In the next post we’ll quantify this balance with CORRA’s fairness metrics and watch the engine rebalance itself live when a session goes off-script.

 

 

Bibliography

Core References (Foundational to CORRA’s methods)

  1. Holyer, I. (1981). The NP-Completeness of Edge-Colouring. SIAM Journal on Computing, 10(4), 718–720.
    The key result proving that finding an optimal edge-colouring (and therefore an optimal round-robin schedule under realistic constraints) is NP-complete.
  2. de Werra, D. (1981). Scheduling in Sports. Annals of Discrete Mathematics, 11, 381–395.
    Canonical treatment of constraint-based sports timetabling, the theoretical basis of fair-play scheduling.
  3. Kirkman, T. P. (1847). On a problem in combinations. The Quarterly Journal of Pure and Applied Mathematics, 2, 191–204.
    The earliest formal statement of the combinatorial “schoolgirl problem”, foundational to balanced tournament design.
  4. Ribeiro, C. C., Urrutia, S., & Noronha, T. F. (2013). Sports scheduling: Problems and applications. International Transactions in Operational Research, 19(6), 767–801.
    Modern survey of algorithmic approaches, including integer programming and heuristic scheduling.
  5. Kendall, G., Knust, S., Ribeiro, C. C., & Urrutia, S. (2010). Scheduling in Sports: An Annotated Bibliography. Computers & Operations Research, 37(1), 1–19.
    Definitive reference list for NP-hard tournament timetabling problems.
  6. Papadimitriou, C. H. (1994). Computational Complexity. Addison–Wesley.
    The foundational textbook defining NP-completeness.
  7. Russell, S., & Norvig, P. (2021). Artificial Intelligence: A Modern Approach (4th ed.). Pearson.
    Greedy heuristics, local optimisation, and search under constraints are fundamental to modern AI design as much as they are to CORRA (Chapters 3–4).

Recommended Reading for Practitioners